A gentle introduction to algorithms
Spoiler: Even if you don’t know how to code, you already know a few algorithms!
Algorithms are at the heart of the technology we see around us. They generate your social media news feed, your Google search results, and the routes you may take daily through navigation apps like Google Maps.
You're ready to start learning about algorithms once you've learned some programming basics in one language. If you feel intimidated by algorithms, the truth of the matter is that you already know a few from elementary school. In fact, algorithms have been used for thousands of years, before programming ever existed.
Today I'll give a gentle introduction to algorithms, covering:
What are algorithms?
How to use and combine algorithms
Which algorithm is “best”?
Your secret weapon: Big O notation
Consider this “lesson 0” on algorithms. Let’s dive in!
What are algorithms?
Put simply, algorithms are a set of steps we take to solve a problem or perform a particular task. While data structures are ways we store data, algorithms are the proven methods we use to solve problems with that data.
For example, this is an algorithm for making an omelet:
Crack eggs into bowl
Whip eggs
Heat pan
Cook eggs in pan
The simplest algorithms are those we learn without even knowing they’re algorithms. In fact, you might be surprised to learn that math formulas are algorithms.
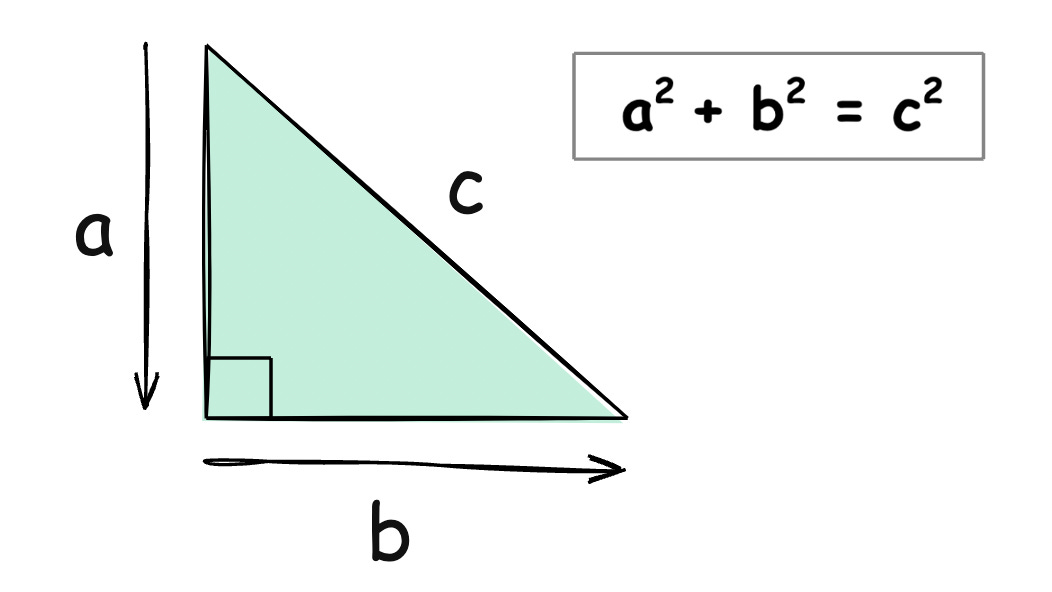
Consider the Pythagorean theorem, which you've likely encountered before. The Pythagorean theorem is a simple algorithm for calculating the length of the hypotenuse of a right triangle (and it has been used since ancient Mesopotamian times).
Imagine: if we didn't have the Pythagorean theorem, we'd have to measure triangles manually. In a similar way, algorithms allow us to efficiently apply mathematical principles like the Pythagorean theorem to solve problems efficiently as programmers.
Math formulas are the inspiration for the algorithms used in modern computing. That said, math formulas have to be turned into machine algorithms (i.e., translated into algorithms that computers understand). This task is the responsibility of a programmer.
> Fun fact: Ada Lovelace is considered the first programmer to have written a machine algorithm.
How to use and combine algorithms
While many algorithms are tried-and-true, new algorithms are constantly being developed.
On your day job, you'll most frequently be using known algorithms to solve problems. With enough experience, you can even make your own algorithms. Being able to write algorithms specific to your problem will help you solve problems even more efficiently than a cookie-cutter algorithm that wasn't written specifically for your job at hand.
If this seems intimidating, just know that you won't be expected to create your own algorithms as a beginner. But when you do, it doesn't have to be as hard as inventing a circle. In fact, you can create new algorithms by simply building upon an established algorithm.
Many algorithms build on each other to solve bigger, more specific problems.
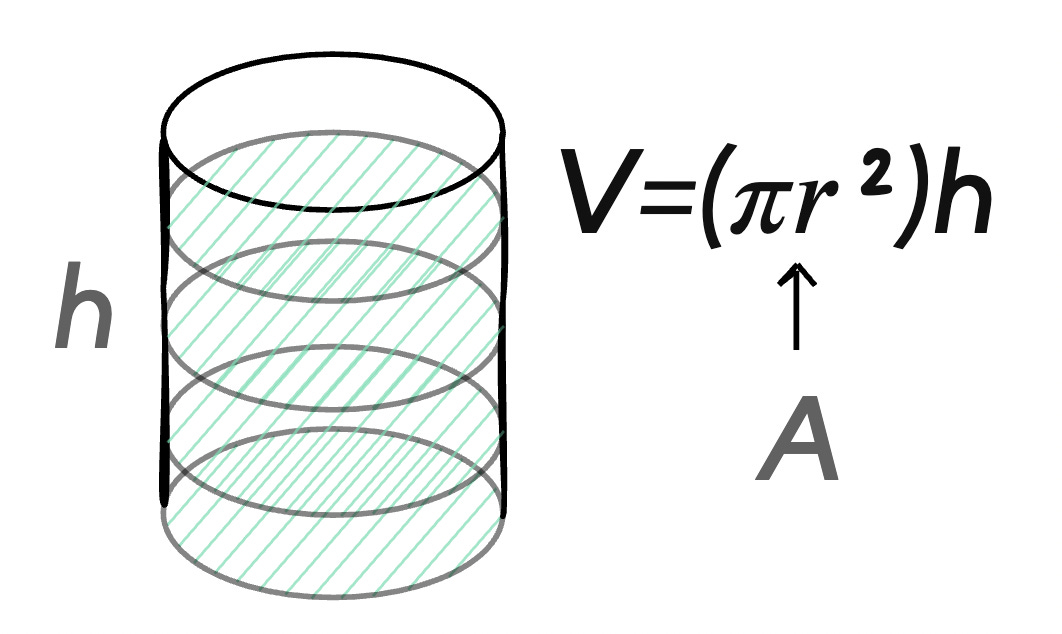
For example, remember the area of a circle (A=𝜋𝑟2)?
We build upon the area of a circle to solve a more complex problem: finding the volume of the cylinder (𝑉=𝜋𝑟2ℎ). What we did here was to extend the algorithm for calculating the area of a circle (A=𝜋𝑟2) to create a more complex algorithm that solves the volume of a cylinder. (𝑉=𝜋𝑟2ℎ)
This is all to say that you don't have to be writing a new theorem as a mathematician to create an algorithm: you can simply build upon what you know, factoring in the needs of your specific problem.
Which algorithm is “best”?
You will start your journey with some basic, introductory algorithms, often focusing on sorting and searching algorithms.
For example:
How to sort an array of numbers
How to search within an array efficiently
How to traverse different data structures quickly.
And here's the thing: often, you can get the same end result from various algorithms.
This means you have to choose which one is the most efficient. And this choice is always subjective to the particular problem at hand.
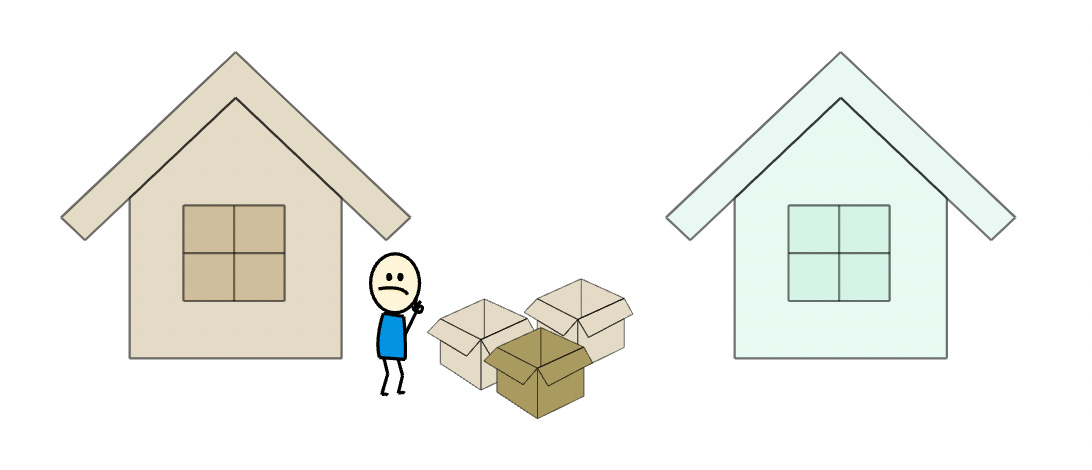
For example, consider the following algorithms for moving furniture between two houses.
Algorithm 1
Take one piece of furniture from house 1
Transport it to house 2
Return to house 1
Repeat steps 1 & 2 until all furniture is moved
Algorithm 2
Take all furniture from house 1
Transport it to house 2
At first glance, it may seem that algorithm 2 is better. You take less trips between houses, so you should be done faster. However, the best algorithm isn't always the one that has the least steps.
Algorithm 2 may take less time, but it will require a massive moving truck to fit the entire house's contents, which might be costly, especially if you're on a budget.
These problems each have different needs, whether material needs (vehicles, money) or time. And this is analogous to what we refer to as different complexities for algorithms.
Early in your journey, you'll be using what's called Big O notation to understand each algorithm's complexity, and compare them to pick the best choice for your problem.
Your secret weapon: Big O notation
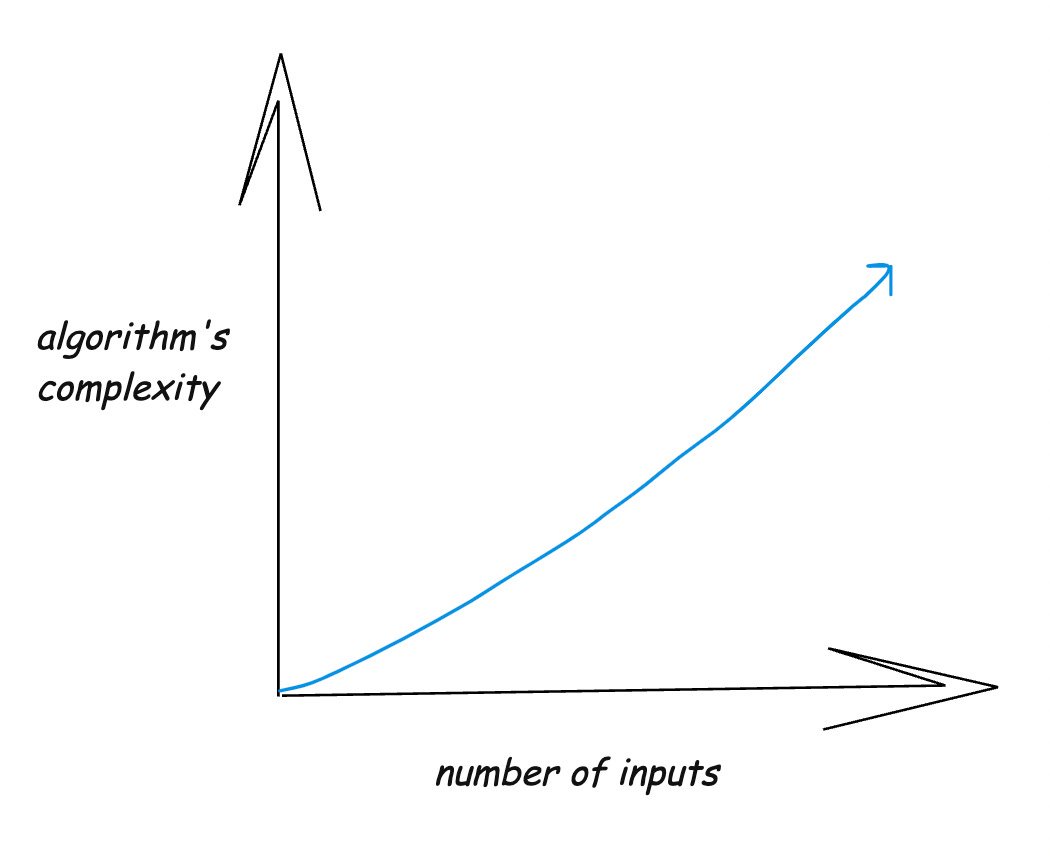
Big O notation is a way to describe how an algorithm's efficiency changes as the amount of data grows. It helps us understand the worst case scenario for:
How many steps an algorithm might take (time complexity)
How much memory it might use (space complexity)
We use Big O to compare algorithms and choose the best one for our needs, ESPECIALLY when dealing with large amounts of data.
When we're dealing with large amounts of data, our algorithms tend to get more complicated. Indeed, the complexity of an algorithm usually depends on the number of inputs.
For instance, if we have to sort just three numbers in order from smallest to largest, there are only three inputs: a, b, and c.
We can use the following algorithm to sort a, b, and c:
Compare the first two (a and b) to see which is greater.
Swap a and b if necessary
Compare the greater of the two with c.
Swap b and c if necessary
If c is greater, we know enough to sort from lowest to highest
If c is NOT greater:
Compare c with the smaller of a and b.
So, we can solve this problem with three inputs with no more than five steps. But if we try to sort five numbers from lowest to highest, the algorithm becomes more complex.
Even the most efficient algorithm, when applied to millions of numbers, will become complex. Whether it's how fast it will be or how much memory it will need, understanding how an algorithm's efficiency will change over time is crucial to making a fully informed choice on which algorithm to opt for.
This is why Big O notation becomes an essential, everyday tool for programmers — but it's not a lesson 0 topic, so we'll wrap up our discussion here.
Ready to build your knowledge of algorithms?
Computers excel at one thing: executing simple instructions. Programmers excel at another: choosing the best algorithm for a given task. Once we give the computer some data (packaged in a data structure), we can use algorithms to elegantly solve problems with that data.
To get hands-on with algorithms, you may want to try the Educative course, A Visual Introduction to Algorithms. This interactive course trains you on the foundations of algorithms, where you'll dive deeper into Big O notation and learn introductory algorithms in your preferred language (e.g., Java, Python, C++ or Javascript).
Happy learning!
- Fahim